Me invitaron a escribir este artículo después de recibir un catálogo de atractivas piezas de ciclo que mencionaban el peso de cada pieza. Los precios parecen aumentar significativamente para artículos que pesan unos pocos gramos menos. Aunque es bueno tener un ciclo atractivo y todo esto definitivamente ayuda Para disfrutar de lo que para la mayoría de nosotros es un deporte recreativo, me preguntaba cuánto marcan la diferencia cien gramos o unas pocas libras.
En primer lugar, tenemos que pensar en algunos parámetros para un ciclista imaginario, así que elegí un peso corporal básico de 80 kg (176,37 lbs) y una bicicleta de 8,5 kg (18,74 lbs). Nuestro ciclista planea hacer un deporte de 50 km. en un período de tres horas. Este evento en particular tiene 1000 m de desnivel, incluidos algunos tramos empinados que son 10% verticales sobre 500 m. El ciclista se dio cuenta de que al mejorar sus ruedas, pedales, manillares, portabotellas y transmisión, podría ahorrar hasta 500 g de peso. Se pregunta qué diferencia haría en su día.
Física del ciclismo en la escuela secundaria
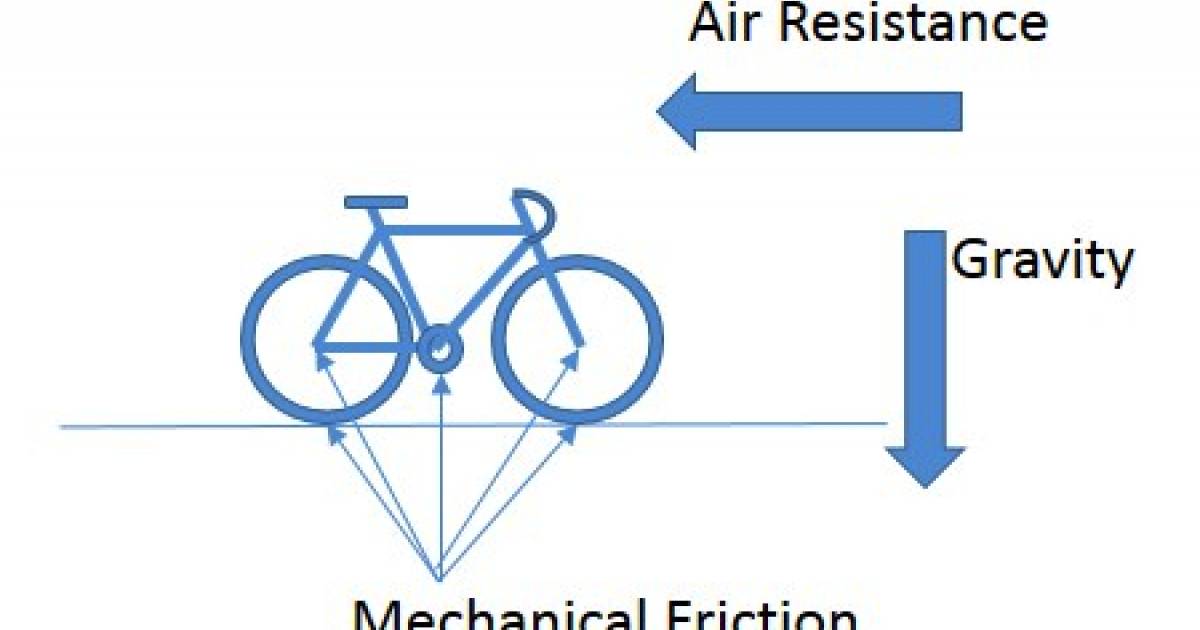
Vamos a volver a una ciencia de secundaria para averiguarlo, primero, las fuerzas que actúan de nuevo el ciclista que tendrá que vencer, estas fuerzas incluyen la gravedad, la resistencia del aire y la resistencia en la cadena cinemática como cojinetes, cadena y neumáticos.
Cuando nuestro ciclista se mueve en llano, la cantidad de esfuerzo o potencia generada corresponde a la energía disipada para vencer el aire y la resistencia mecánica (dejo el aire y la resistencia mecánica a otro elemento por ahora). A la velocidad constante, todos estos Las fuerzas estarán equilibradas y el ciclista producirá suficiente energía para mantenerlas todas en equilibrio.
Volviendo a nuestra ciencia de la escuela secundaria, el ciclista tiene una energía cinética inherente debido a la velocidad del ciclo y el ciclista a lo largo del suelo y la rotación de las ruedas:
Ke – 1/2 m. V2
Donde es la masa combinada del ciclista y el ciclo y V es la velocidad.
Ke – 1/2 m. r. w2
Donde es la masa de la rueda, r es el radio yw es la velocidad de rotación. Esto en realidad es una simplificación porque depende de cómo se distribuye el peso de la rueda entre la llanta y el cubo.
Si los ciclistas andan libremente, entonces esta energía cinética se disipará para superar la resistencia del aire y la fricción mecánica y disminuirán la velocidad. fuerza de gravedad que solo entrará en vigor cuesta arriba o cuesta abajo.
La física del descenso
¿Qué pasa cuando bajamos? Siempre tenemos las mismas fuerzas actuando sobre el ciclista, esta vez, sin embargo, hay un componente de fuerza gravitacional que lo ayuda a bajar la colina, para simplificar, asumiremos que después de subir una de las pendientes pronunciadas, decide bajar libre, utilizando su energía potencial adquirida durante la escalada.
Si recuerda, la energía potencial perdida es:
Pe – m. G. h
Donde es la masa combinada del ciclista y el ciclo, G es la constante gravitacional y h es el cambio de altura.
La energía cinética que se gana cuando llega al fondo es:
Ke – 1/2 m. V2 1/2 m. r. w2
También se perderá algo de energía al superar la fricción mecánica y del aire a medida que se acelera cuesta abajo. Dado que Pe y Ke incluyen la masa combinada del ciclista y el ciclista, un cambio de peso no tendrá ningún efecto sobre la velocidad del ciclista Si no quieres seguir el cálculo, recuerda a Galileo, de quien se dice que dejó caer dos masas diferentes de la Torre de Pisa en 1589 para demostrar que aterrizarían al mismo tiempo. Desde cualquier ventaja mecánica o aerodinámica, algunas piezas nuevas para ganar peso no parecen hacer ninguna diferencia en el rendimiento de nuestro ciclista en llano o cuesta abajo.
La física de la escalada
¿Qué pasa cuando subimos una colina? Para ilustrar lo que sucede en este escenario, imagina que nuestro ciclista sube uno de los 10% de caída vertical sobre 500 m. Para simplificar, mantiene una velocidad constante de 10 km / h para ganar 50 m de altura. minutos (180 segundos) para subir la costa.
Como no hay cambio en su velocidad, la energía cinética permanece constante, requiriendo algún esfuerzo para compensar el aire y la fricción mecánica, sin embargo, debe levantar su peso de 50 m durante este tiempo. Tomando nuestras cifras originales de 88. 5 kg para el combinado. peso del ciclista y la bicicleta, el cambio de energía potencial será:
Pe – 88,5 x 9,81 x 50 – 43,409 julios
Durante tres minutos (180 segundos), esto equivale a un esfuerzo constante de 241 vatios. Al reducir el peso de la bicicleta en 500 g, el esfuerzo necesario para subir la costa a la misma velocidad es ahora:
Pe – 88 x 9,81 x 50 – 43,164 julios
Esto equivale a un esfuerzo constante de 239 vatios durante tres minutos, o dos vatios de diferencia. Reorganizar las fórmulas para calcular el tiempo que se tarda en subir la misma colina a 241 vatios con un peso reducido (88 kg frente a 88,5 kg) da 179 segundos , que es un segundo más rápido. Durante nuestro viaje más largo, que tiene mil metros de desnivel, sería como veinte segundos más rápido.
La física de parar y arrancar
En realidad, la mayoría de mis salidas no son tramos a velocidad constante, hay frecuentes cambios de tempo o paradas y arranques, por lo que el último escenario que me gustaría ver es casi detenerme y luego volver a acelerar a mayor velocidad.
Me imagino que nuestro ciclista acelera en una superficie plana desde el reposo mientras aplica 400 vatios (400 julios por segundo) de esfuerzo, espero que no sea demasiado. Esta vez, debemos observar la ganancia de energía cinética necesaria para mover al ciclista y andar en bicicleta y hacer girar las ruedas. Se supone que las ruedas y los neumáticos tienen una masa de 1,5 kg y un radio de 33 cm.
Para volver a nuestras ecuaciones originales y reorganizar algunos elementos para calcular la velocidad al final del primer segundo:
Ke – 1/2 m. V2 1/2 m. r. w2 – 1/2 m. (V2 V2 / r) – 1/2 m. (V2). (1 1 / r)
V2 – Ke. 2 / m. r / (1 r)
V – raíz cuadrada de [Ke. 2 / m. r / (1 r)]
Después del primer segundo:
V – raíz cuadrada [400,2 / 88,5. (0,33 / 1,33)] 1,5 m / so 5,3 km / h
Pasados dos segundos, nuestro conductor habrá aportado 800 julios y por tanto la velocidad (independientemente de la resistencia del aire y la fricción) será de 2,1 m / so 7,6 km / h. Nótese que la progresión no es lineal debido a la raíz cuadrada. proceso para 88,5 kg y nuestro ahorro de peso propuesto de 500 g da la siguiente tabla:
Aunque esto ha sido una simplificación al ignorar la resistencia del aire y la fricción (algunos de estos 400 vatios se utilizarán para compensar estas pérdidas a medida que nuestro ciclista acelere), las ganancias son bastante pequeñas, por lo que una ganancia de peso de 500 g daría algunas ganancias marginales en aceleración y subida, que pueden acumularse durante un viaje más largo con varias paradas y salidas y subidas importantes , ahorrando uno o dos minutos.
El peso del propio ciclista
Después de ver el ciclo, ahora mire brevemente al ciclista, si después de mirarse al espejo una mañana, el ciclista decide que podría perder 6 kg (casi una piedra) de peso innecesario, los resultados son un poco más significativos. ahora pesa 74 kg y la bicicleta se mantiene en 8,5 kg, para un peso combinado de 82,5 kg
Subiendo la pendiente de 500 ma 10%, Pe – 82,5 x 9,81 x 50 – 40,466 julios, requiriendo 225 vatios – o dieciséis vatios menos ¿Ha intentado mejorar su potencia en dieciséis vatios?Ciertamente vale la pena ahorrar, manteniendo la potencia en 241 vatios, llegaría a la cima de la colina en 168 segundos, o doce segundos antes, durante nuestra larga caminata con 1000m de caída vertical, esto equivaldría a ser cuatro minutos más rápido.
En el escenario acelerado, después de solo unos segundos, el ciclista es casi medio kilómetro por hora más rápido:
Entonces, si está buscando ir más rápido sin entrenamiento, a veces se trata del conductor, no de la bicicleta. En cuanto a estas sofisticadas piezas de bicicleta, es mejor que guarde la billetera o el bolso.